Os círculos gêmeos de Arquimedes

No livro dos Lemas de Arquimedes aparecem os problemas dos arbelos (faca de sapateiro), que é a região limitada por dois semicírculos tangentes entre si e a um terceiro semicírculo maior, cujo diâmetro é a soma dos dois menores. Os círculos gêmeos de Arquimedes estão ligados diretamente ao problema dos arbelos.

Os círculos gêmeos de Arquimedes são dois círculos tangentes aos dois semicírculos menores, ao maior e a um segmento de reta perpendicular ao ponto de tangência entre os dois semicírculos menores.

Para quaisquer raios que o dois semicírculos menores assumam, os raios dos círculos gêmeos serão sempre iguais e, consequentemente, suas áreas.

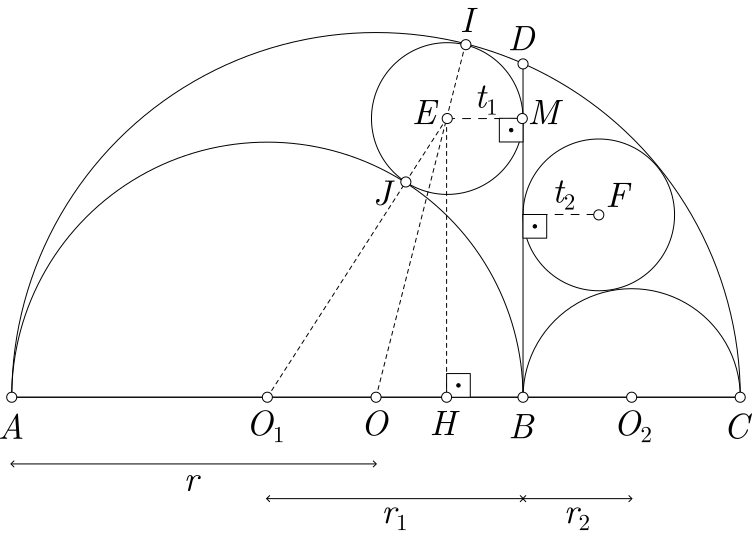
Seja um semicírculo de centro $O$ e raio $r$, com diâmetro definido como $AC$ e sejam outros dois semicírculos menores de centros $O_1$ e $O_2$, raios $r_1$ e $r_2$ e diâmetros $AB$ e $BC$, respectivamente.

Traçamos por $B$ um segmento de reta $BD$ perpendicular ao diâmetro $AC$, marcando o ponto $D$ na intersecção com o semicírculo maior.

Descrevemos dois círculos de raios $t_1$ e $t_2$, com centros $E$ e $F$, respectivamente, de modo que o círculo de centro $E$ seja tangente ao segmento $BD$ e aos semicírculos de diâmetros $AC$, e $AB$; e o círculo de centro $F$ seja tangente ao segmento $BD$ e aos semicírculos de diâmetros $AC$ e BC$.

Vamos provar que:

• A distância de $E$ ao segmento $AC$ é dada por:

$$
EH = \sqrt{(r_1+r_2)^2 - (r_1-t_1)^2} \tag{1}
$$

• Os raios dos dos círculos gêmeos de Arquimedes são dados por:

$$
t = \frac{r_1 \cdot r_2}{r_1 + r_2} \tag{2}
$$

Demonstrações:

Para encontrarmos algumas relações que nos ajudem a provar $(1)$ e $(2)$, fazemos

• Traçamos o segmento $HE$, perpendicular ao diâmetro $AC$;
• Traçamos o segmento $OE$, marcando como $I$ a intersecção com o semicírculo de centro $O$;
• Traçamos os segmento $O_1E$, marcando como $J$ a tangência entre o semicírculo de centro $O_1$ e o círculo de centro $E$;
• Traçamos o segmento $EM$ perpendicular ao segmento $BD$.

Prova de (1):

Como o segmento $AC = AB + BC$, segue que:

$$
r = r_1 + r_2 \tag{3}
$$

Do segmento $O_1E$, temos:

$$
O_1E = O_1J + JE\\
\ \\
O_1E = r_1 + t_1 \tag{4}
$$

Do segmento $OI$, temos:

$$
EO = OI - EI\
\ \\
EO = r - t_1 \tag{5}
$$

Do segmento $O_1H$, temos:

$$
O_1H = O_!B - HB\\
\ \\
O_1H = O_1B - EM\\
\ \\
O_1H = r_1 - t_1 \tag{6}
$$

Do segmento $OC$, temos:

$$
OH = OC - HB - BC\\
\ \\
OH = (r_1+r_2) - t_1 - 2r_2\\
\ \\
OH = r_1 + r_2 - t_1 - 2r_2\\
\ \\
OH = r_1 - r_2 - t_1 \tag{7}
$$

Aplicamos o Teorema de Pitágoras no triângulo $EO_1H$ e substituímos as relações $(4)$ e $(6)$:

$$
O_1E^2 = EH^2 + O_1H^2\\
\ \\
EH^2 = O_1E^2 - O_1H^2\\
\ \\
EH^2 = (r_1+t_1)^2 - (r_1-t_1)^2\\
\ \\
EH = \sqrt{(r_1+t_1)^2 - (r_1 - t_1)^2} \tag{8}
$$

Prova de (2):

Aplicamos o Teorema de Pitágoras no triângulo $EOH$ e substituímos as relações $(5)$ e $(7)$:

$$
EO^2 = EH^2 + OH^2\\
\ \\
EH^2 = EO^2 - OH^2\\
\ \\
EH^2 = (r-t_1)^2 - (r_1 - r_2 - t_1)^2
$$

Mas, $r=r_1+r_2$. Assim:

$$
EH^2 = (r_1+r_2-t_1)^2 - (r_1-r_2-t_1)^2 
$$

Substituindo a relação $(8)$ na relação acima, obtemos:

$$
\color{red}{(r_1+t_1)^2} - \color{blue}{(r_1 - t_1)^2} =\\
\color{green}{(r_1+r_2-t_1)^2} - \color{magenta}{(r_1-r_2-t_1)^2} \tag{9}
$$

Vamos aplicar o produto notável em cada quadrado da igualdade acima separadamente para facilitar a visualização:

$$
\color{red}{(r_1+t_1)^2 = r_1^2 + 2r_1t_1 + t_1^2}
\ \\ \ \\
\color{blue}{(r_1-t_1)^2 = r_1^2-2r_1t_1 + t_1^2}
\ \\ \ \\
\color{green}{(r_1+r_2-t_1)^2 = r_1^2+2r_1r_2-2r_1t_1+\\ r_2^2-2r_2t_1+t_1^2}
\ \\ \ \\
\color{magenta}{(r_1-r_2-t_1)^2 = r_1^2 - 2r_1r_2 - 2r_1t_1 + \\ r_2^2 + 2r_2t_1 + t_1^2}
$$

Agora, aplicamos em $(9)$ os produtos notáveis em sua forma expandida:

$$
r_1^2 + 2r_1t_1 + t_1^2 - r_1^2+2r_1t_1 - t_1^2 = \\
r_1^2+2r_1r_2-2r_1t_1+ r_2^2-2r_2t_1+t_1^2 - \\
r_1^2 + 2r_1r_2 + 2r_1t_1 - r_2^2 - 2r_2t_1 - t_1^2
$$

Através de um pouco de álgebra, somamos os termos comuns e cancelamos termos opostos:

$$
4r_1t_1 = 4r_1r_2 - 4r_2t_1\\
\ \\
4r_1t_1+4r_2t_1 = 4r_1r_2\\
\ \\
4t_1(r_1+r_2) = 4r_1r_2
$$

Finalmente obtendo:

$$
t_1 = \frac{r_1 \cdot r_2}{r_1+r_2} \tag{10}
$$

De modo análogo, considerando as projeções de $F$ sobre os segmentos $BC$ e $BD$, podemos provar que:

$$
t_2 = \frac{r_1 \cdot r_2}{r_1+r_2} \tag{11}
$$

Sendo assim, as relações $(10)$ e $(11)$ mostra que $t_1=t_2$, provando que os círculos gêmeos de Arquimedes possuem raios iguais e, portanto, áreas iguais. Assim, podemos escrever:

$$
t = \frac{r_1 \cdot r_2}{r_1+r_2}
$$

Veja mais:

• O teorema da corda quebrada de Arquimedes
  
• Arquimedes e a área do círculo
  
• Sobre a esfera e o cilindro
• O corpus arquimediano
  
• 7 matemáticos gregos no blog do Professor Edigley Alexandre
  

Livros sobre Arquimedes na Amazon: